Agnostische Modellierung von Werten aus der Realität
An diesem Tag in der schönsten aller möglichen Welten beschäftigen wir uns mit Zahlen aus der Realität.
Betrachten Sie einen Aspekt der Realität, der sich gut in Zahlen übertragen lässt.
Nehmen Sie an, Sie codieren einen Aspekt der Realität in einen Wert \(X\).
Das erfordert eine Übersetzungsleistung von Ihnen.
Sie müssen auf irgendeine Art messen.
Sie könnten auch zählen, aber lassen Sie uns für diesen Blog annehmen, dass Ihre Zahl kontinuierliche Werte annimmt und nicht von ganzer Zahl zu ganzer Zahl springt. Eine Betrachtung solcher (Zähl-)Prozesse ist auch sehr fruchtbar, wird heute aber nicht unser Thema sein.
Mögliche Beispiele für solche Werte:
- Position eines Staubteilchens in einem Wasserbottich.
- Tonlautstärke eines Radios während statischen Rauschens.
- Kleine Schwankungen des menschlichen Körpers während des Gehens oder Stehens aufgrund von kleinen Muskelzuckungen.
- etc.
Egal, was die Zahl \(X\) nun für Sie bedeutet, sie ändert sich mit der Zeit.
Heute beschäftigen wir uns mit der Frage:
Wie ändert sich der Wert \(X\) nun mit der Zeit?
Eine allgemeine Antwort übersteigt meine Fähigkeiten.
Deshalb setzen wir uns mal mit Strukturen auseinander, welche ein Modell zur Beschreibung solcher Werte haben kann.
Im heutigen Blogpost werde ich Ihnen ein Theorem vorstellen, welches zulässt, agnostisch auf ein sehr konkretes Modell zu schließen.
Dazu motiviere ich zunächst, warum wir über Wahrscheinlichkeiten sprechen, danach führen wir Definitionen ein, um dann die Kernaussage formulieren zu können.
Sobald diese steht, erkläre ich, wie eine Anwendung des Arguments in einer angewandten Wissenschaft funktionieren kann.
Daran werde ich illustrieren, was Mathematik den angewandten Wissenschaften unter anderem bieten kann.
Weshalb Wahrscheinlichkeit?
Behalten Sie Ihren Wert aus der Realität im Kopf.
Wir möchten über die Struktur eines möglichen Modells sprechen. Da stellt sich die Frage, nach welchen grundlegenden Mustern Ihr Wert in der Realität zustande kommt.
Nehmen wir einmal an, Gott würde würfeln, wenn er die Realität erschafft. Dann müssen wir über Zufall sprechen.
Auch wenn Sie auf einer theologisch grundverschiedenen Position ausharren möchten, dann sollten wir es trotzdem tun.
Weshalb? Hier sind vier Gründe:
- Es ist praktisch.
- Es ist sehr hübsch.
- Sie möchten die Möglichkeit von deterministischer Natur und einer vollständig deterministischen Grundwahrheit in dem von Ihnen in Daten übersetzten Teil der Realität verteidigen? Dann müssen Sie doch trotzdem anerkennen, dass der Mensch und damit wir diese auf gar keinen Fall verstehen.
Dazu sind wir viel zu grobmotorisch veranlagt. Machste nix. Muss man sich zurückziehen. Wenn man es nicht exakt weiß, dann muss man anfangen, über Wahrscheinlichkeiten zu sprechen. Und dann sind wir auch wieder beim Zufall, dieses Mal nur mit einer anderen Herleitung. - Ich kenne mich damit aus (ein bisschen).
Definitionen
Der von Ihnen aus der Realität abgemessene Wert \(X\) ändert sich mit der Zeit.
Um dies zu kennzeichnen, führen wir nun den Index \(t\) ein (\(t\) für Zeit).
Nun bedeutet \(X_t\) der Wert von Ihrer ausgewählten Messung \(X\) zum Zeitpunkt \(t\).
Wir beginnen unsere Zeitrechnung sehr willkürlich mit der \(0\) und nehmen an, wir kennen den Startwert \(X_0\).
Für jede Zeit \(t\) in der Zukunft \(t>0\) wird unser \(X_t\) einen Wert haben.
Eine solche Zuordnung von einer Zeit \(t\) zu einem Wert \(X_t\) nennt man eine Funktion.
Ein Beispiel für eine solche Funktion kennen Sie aus dem Schulunterricht.
Man nennt sie auch Pfade.
Ein paar Beispiele sind in Abbildung @ref(fig:brownian) illustriert.
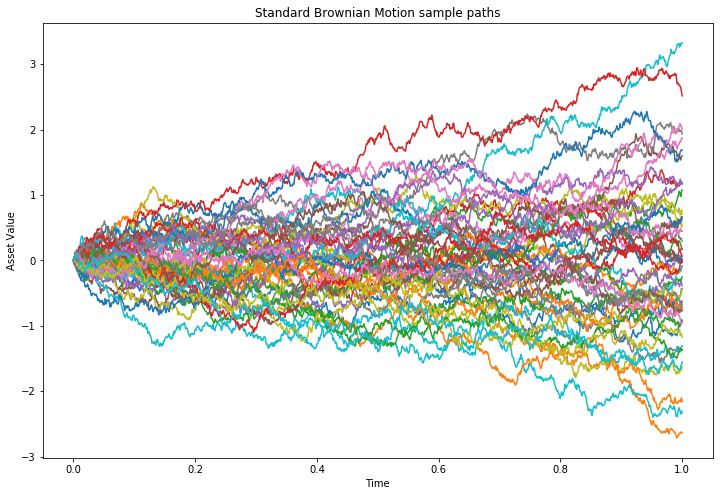
Wir wissen, wo die Funktion \(X_t\) beginnt.
Wie geht sie weiter?
Egal, welchen Bezug Ihre Zahl \(X_t\) nun zur Realität hat und egal, wie Ihre grundlegende Annahme über die Natur der Wirkmechanismen treffen, ist eines doch klar:
Es genau auszurechnen, wird brutal kompliziert.
Mein persönlicher Tipp deshalb: nicht versuchen!
Außer, Sie werden enorm gut bezahlt dafür.
Nehmen wir einmal das erste Beispiel aus der obigen Sammlung: Um die genaue Position des Staubteilchens zu einem späteren Zeitpunkt auszurechnen, müssten Sie die Bewegungen eines jeden Wassermoleküls um das Staubteilchen herum verstehen und die Kollision zwischen Molekül und Staubteilchen für jedes einzelne berechnen.
In einem Wasserbottich sind etwa \(10^{23}\) Teilchen. Das sind sehr viele.
Ich weiß nicht, wer da noch glücklich wird.
Daher treten wir nun den geordneten Rückzug an: Wir modellieren stochastisch. Anstatt exakten Aussagen treffen wir nun nur noch Aussagen über Wahrscheinlichkeiten.
Jeder Zuwachs der Zahlen zwischen zwei Zeitpunkten \(t\) und \(s\) mit \(t>s\) wird notiert mit \(X_t-X_s\) und ist nun zufällig.
Wir nehmen jetzt zusätzlich an, dass die Funktion über die Zeit \(X_t\) kontinuierlich ist.
Im Grunde genommen bedeutet das, dass der Wert \(X_t\) nicht abrupt springt, während er sich in der Zeit verändert, sondern sich nur kontinuierlich bewegt.
Beachten Sie, dass die bisher von uns verfolgten Überlegungen sehr agnostisch waren:
- Kein Gott wurde angenommen, weder ein würfelnder Gott noch ein sonstiger Gott (für die weitere Diskussion völlig irrelevant).
- Wir haben keine Annahme über den Ursprung der Zahlen getroffen. Wir haben ausschließlich angenommen, dass sie sich stetig in der Zeit verändern. Dieser Punkt schließt Zählprozesse aus.
- Wir haben angenommen, dass wir den Anfangspunkt kennen.
Trotz dieser wenigen und wenig spezifischen Annahmen können wir die folgende Aussage treffen:
Es besteht eine Äquivalenz zwischen den folgenden Aussagen:
Für alle beliebigen Zeiten \(t,s,v,j\geq 0\) mit \(t>s>v>j\) gilt, dass die Zuwächse \(X_t-X_s\) und \(X_v-X_j\) unabhängig voneinander sind.
Das bedeutet, dass aus der genauen Kenntnis des einen Wertes keine Information über den anderen Wert gezogen werden kann.\(X_t\) ist ein sogenannter Gaußprozess, genauer gesagt ist für alle \(t,s \geq 0\) mit \(t>s\) die Wahrscheinlichkeitsverteilung des Zuwachses \(X_t-X_s\) normalverteilt.
Mit anderen Worten: die Wahrscheinlichkeit, dass \(X_t-X_s\) zwischen zwei Zahlen \(a\) und \(b\) liegt (\(a<b\)), ist [ _a^b e^{-},dx. ] Die Parameter \(\sigma(t,s)\) und \(\mu(t,s)\) sind gegeben durch zwei Funktionen. Die sogenannte Mittelwertsfunktion \(m(t)\) ordnet jeder Zeit \(t\) eine Zahl zu. Da wir bereits den Anfangswert \(X_0\) kennen, so ist \(m(0)=X_0\). Dann ist \(\mu(t,s)=m(t)-m(s)\).
Darüber hinaus gibt es die Varianzfunktion \(u(t)\), welche jeder Zeit eine Varianz, also eine positive Zahl, zuordnet. Da die Unsicherheit mit der Zeit zunimmt, ist die Varianzfunktion wachsend in der Zeit. Dann ist \(\sigma(t,s)^2=u(t)-u(s)\). Beide Funktionen \(u\) und \(m\) sind stetig.
Also, wenn (A) auf \(X_t\) zutrifft, dann trifft auch (B) auf \(X_t\) zu und vice versa. Alternativ formuliert: wenn (A) nicht auf \(X_t\) zutrifft, so trifft auch (B) nicht auf \(X_t\) zu und vice versa.
Man nennt eine solche Aussage über die Beziehung zweier Aussagen (A) und (B) Äquivalenz und notiert \((A) \Leftrightarrow (B)\).
Anwendungen des Theorems
Für die Anwendung machen wir es zuerst konkret und danach abstrakt.
Steigen wir ein mit dem dritten oben genannten Beispiel:
Denken Sie an die Muskelzuckungen, welche zu kleinen Schwankungen des menschlichen Körpers führen. Wenn Sie jetzt annehmen, dass die Muskelzuckungen in den nächsten 10 Sekunden nichts mit denen in den darauffolgenden 10 Sekunden zu tun haben und auch nix mit denen in einer Minute, dann können Sie ganz schön viel sagen:
Sie können einen sehr genauen Ausdruck für die Wahrscheinlichkeiten für die Position nach einer Zeit angeben.
Natürlich fehlen hier noch zwei essentielle Informationen: \(m(t)\) und \(u(t)\). Diese beiden Funktionen müssen aus Messungen deduziert werden. Damit beschäftigt sich die Statistik.
Doch die Struktur der Wahrscheinlichkeiten ist vollständig geklärt.
Abstrakt sieht eine Anwendung des obigen Theorems in einer angewandten Wissenschaft in etwa wie folgt aus:
Betrachte einen aus der Realität gemessenen Wert, welcher sich stetig in der Zeit ändert. Aus realitätsnahen Überlegungen kommen Sie zu dem Schluss, dass die Zuwächse dieses Wertes unabhängig voneinander sind. Durch das obige Theorem kennen Sie nun die Form der Wahrscheinlichkeitsverteilung. Weil Sie nun wissen, wie die Struktur aussieht, können Sie die fehlenden Informationen aus den Daten schätzen. Damit Sie das dann auch wirklich können, lernen Sie das in Statistik (hoffentlich).
Das Argument könnte auch herumgedreht werden:
Weil eine Verteilung der obigen Struktur enorm gut zu einem aus der Realität gemessenen Wert passt, kann mit Hilfe des Theorems auf eine Unabhängigkeit der Zuwächse geschlossen werden.
Natürlich nur im Rahmen aller Unsicherheiten, die eine Auseinandersetzung mit der Realität eben so mit sich bringt.
Nun noch einmal zur Wiederholung und Gewöhnung das obige Theorem in mathematischer Schreibweise:
Theorem von Paul Lévy
Sei \((X_t)_{t\in [0,\infty)}\) ein stochastischer Prozess mit Werten in \(\mathbb{R}\); sei \(X_0=a \in \mathbb{R}\) und \(X_t\) habe stetige Pfade, beides mit Wahrscheinlichkeit \(1\).
Dann besteht Äquivalenz zwischen:
\(X\) hat unabhängige Inkremente (Zuwächse).
\(X\) ist ein Gauß-Prozess; \(X_t-X_s \overset{d}{=} N(m(t)-m(s),u(t)-u(s))\) für alle \(t,s\geq 0\), \(t\geq s\); wobei \(m(t)\) stetig und \(m(0)=a\); \(u(t)\) monoton wachsend, stetig und \(u(0)=0\).
Schlussbetrachtungen
Zum Schluss nun noch ein paar abschließende Kommentare:
Das obige Theorem hat absoluten Wahrheitswert.
Wenn es in der Wissenschaft wie in der Biologie angewendet wird, dann resultieren alle Unsicherheiten aus der folgenden Frage:
Erfüllt der aus der Realität abgeleitete Wert \(X_t\) die im Theorem gestellten Voraussetzungen?
Jede Beantwortung dieser Frage muss mit Mitteln der jeweiligen Wissenschaft geklärt werden und ist mit Unsicherheit behaftet.
Diese Anwendung illustriert gut, was Mathematik den angewandten Wissenschaften unter anderem bieten kann:
Mathematik kann vorgefertigte Schlussfolgerungsketten bieten, welche – sind sie denn einmal verstanden und ausformuliert – durch strukturelle Einfachheit und Klarheit bestechen.
Natürlich ist es ein hoher Anspruch der Mathematik, diese Einfachheit und Allgemeingültigkeit in ihren Aussagen zu haben, und wir scheitern jeden Tag an unserer Unfähigkeit, gute Antworten zu geben.
Doch sollte man Unfähigkeit nicht zu Unwilligkeit umdeuten und behaupten, Mathematik würde sich mit sophistischen Konvergenzbeweisen beschäftigen, die am Ende niemanden interessieren.
Hoffentlich sind Sie aber heute ein lebendiges Gegenbeispiel: hoffentlich haben Sie etwas gelernt, das zugleich philosophisch interessant ist wie auch möglicherweise von praktischer Relevanz für Ihre Wissenschaft.